Kövek Kopásának modellezése iterált függvényrendszerekkel – korlátok és lehetőségek
Ez a dolgozat az “Élein szelt poliéderek kombinatorikus és metrikus tulajdonságai” című TDK munka (BME Építészmérnöki Kar, 2020) folytatásának eredményeit mutatja be. Az előző dolgozat olyan poliédereket vizsgált, melyek összes csúcsát újra és újra levágjuk egy-egy síkkal, amely sík csakis az adott csúcsból kiinduló éleket metszheti és a levágott gúlák közül semelyik kettőnek nincs közös pontja. Az így létrejövő egyszerű poliéderek, lapjainak átlagos csúcsszáma hat, lapjainak és csúcsainak száma megadható a kezdeti poliéder élei számának függvényeként, önhasonló lapszerkezetük fraktál tulajdonságokat mutat. A csúcsból kiinduló éleket λ<1/2 arányban osztó vágó sík esetén, megadható a kiinduló lap és a lap határalakzatának területének aránya. Ugyanakkor szabályos sokszögből kiindulva kör határalakzat csakis a 2λ=1/(1+cos(ϕ) ) érték esetén lehetséges.
Jelen dolgozat célja az élein szelt poliéderek fraktál tulajdonságainak vizsgálata. Kiegészíti az előző TDK-ban felállított modellt: a csúcsokból kiinduló élek λ_i arányban kerülnek levágásra, míg az újonnan létrehozott éleket γ_i arányban osztja az él határalakzatra kerülő pontja. Az így létrejővő poliéderek geometriája előállítható véletlen iterált függvényrendszerrel (IFS). A meghatározásra kerülő függvényrendszert alkalmazva egy négyzetes csúcs környezetének ábrázolására Matlab algoritmust prezentál.
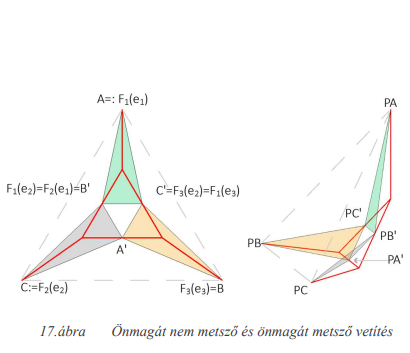
Az IFS általános esetben csak három dimenzióban működik. Bizonyos esetekben azonban- melynek feltételei és egy példa is bemutatásra kerül – az alakzat valamely síkra vetített képe két dimenzióban is előállítható ilyen módon. A létrejövő alakzat lapjait határoló görbék megfelelően konstruáltak, hogy bármely λ_i,γ_i kombinációra első rendben differenciálhatók legyenek. Magasabb rendű differenciálásuk csakis akkor lehetséges, ha a γ_i =λ_i=1/2.
A poliéder lapszerkezetében fraktál tulajdonságokat eredményez, ha a vágó sík éleket távolít el a kezdeti poliéderről. Ennek az eseménynek a vizsgálata IFS-vel több problémát is felvet.