Tarnai Tibor

Születési adatok: 1943. szeptember 28. (Hatvan)

Tanulmányok:

1961 – Bajza József Gimnázium, Hatvanban érettségizett

1966 – okleveles mérnök, Építőipari és Közlekedési Műszaki Egyetem

1973 – okleveles alkalmazott matematikus, Eötvös Loránd Tudományegyetem

1977 – műszaki doktor, Budapesti Műszaki Egyetem,

Értekezés címe: Síkbeli rácsos tartók stabilitása: Párhuzamos övű tartók kifordulása

1980 – a műszaki tudomány kandidátusa,

Értekezés címe: Rúdszerkezet Lokális stabilitásának vizsgálata operátornyalábokkal: Nyitott keresztmetszetű rudak kifordulása

1991 – a műszaki tudomány doktora,

Értekezés címe: Kinematikailag határozatlan szerkezetk és szerkezeti topológia

1995 – a Magyar Tudományos Akadémia levelező tagja

Székfoglaló előadás címe: A szerkezeti mechanika és a társtudományok

2001 – a Magyar Tudományos Akadémia rendes tagja

Székfoglaló előadás címe: Hajtogatott szerkezetek

Munkahelyek, beosztás, feladatok:

1966-70: Földalatti Vasút Vállalat, mérnök, műszaki ellenőr (Fővárosi útépítések, Baross téri alul- és felüljáró építés)

1970-72: Budapesti Városépítési Tervező Vállalat, statikus tervező (Acél és vasbeton szerkezetek: 2 üzletház, 1 szolgáltatóház, 1 fedett uszoda – Újpesti Tisztasági Fürdő, 1 ipari üzemépület és csarnok)

1972-75: Szegedi Tervező Vállalat, statikus irányító tervező (blokkos és paneles lakóépületek, a Gyulai Húskombinát mélyépítési műtárgyai, az Erfurt Rieth Strasse sportcsarnok statikus tervei)

1975-78: Budapesti Városépítési Tervező Vállalat, statikus irányító tervező, szakértések ( idős épületek állagfelmérése, bauxitbeton épületek ellenőrzése, épületkárok véleményezése, statikus tervek épületfelújításokhoz)

1978-1991: Építéstudományi Intézet, tudományos főmunkatárs (Építőipari szerkezetkutatások, szabványelőkészítési céllal acéloszlopok teherbírásának vizsgálata, kinematikailag határizatlan szerkezetek tulajdonságai, ststikus szakvélemények)

1991-93: MTA Műszaki Mechanikai Tanszéki Kutatócsoport, tudományos tanácsadó (Stabilitáselmélet és szerkezeti topológia kutatások)

1993-: BME Építőmérnöki Kar, Mechanika Tanszék, később Tartószerkezetek Mechanikája Tanszék, egyetemi tanár (Statika, Rugalmasságtan tárgyak előadója, Tartók Statikája, Szilárdságtan, Dinamika tárgyak oktatása, Jelenleg: BSc képzésben Statika, MSc képzésben Mechanika tárgyak előadója, PhD képzésben Szerkezeti Topológia és gráfelmélet, Felületszerkezetek tárgyak oktatója, OTKA kutatások irányítója)

2000-2009 Építőmérnöki Doktori Iskola vezetője

Ösztöndíjak:

University of Cambridge, Department of Engineering, UK, magyar állami ösztöndíj, 1978 (3 hónap); Cornell University; Stanford University, USA, IREX Fellowship, 1986-87 (6 hónap); University of Cambridge,UK, Royal Society Guest Research Fellowship, 1990 (9 hónap); University of Tokyo, Inst. of Industrial Science, Japan, JSPS Invitation Fellowship, 1994 (1 hónap); University of Kyoto, Dept.of Environmental Design, Japan, JSPS Invitation Fellowship, 1997 (1 hónap); Széchenyi Professzori Ösztöndíj 1997-2000; University of Kyoto, Dept. of Architecture, Japan, Kajima Fellowship, 2001 (1 hónap); Magdalen College, Oxford, UK, Visiting Fellowship, 2004 (3 hónap); Zhejiang University, Space Structures Research Centre, China, Visiting Fellowship, 2005 (1 hónap);

Kiemelkedő publikációk (5):Cikkek:

–Summation theorems concerning critical loads of bifurcation. Chapter 2 in Structural Stability in Engineering Practice (Ed.: L. Kollár). E & FN Spon, London, 1999, pp 23-58.
-Tarnai, T. and Gáspár, Zs.: Packing of equal regular pentagons on a sphere. Proc. Roy. Soc. Lond. A 457 (2001), 1043-1058. IF: 1.188
-Zero stiffness elastic structures. International Journal of Mechanical Sciences 45 (2003), 425-431. IF: 0.873
-Kovács, F., Tarnai, T., Fowler, P.W., and Guest, S.D.: A class of expandable polyhedral structures. International Journal of Solids and Structures 41 (2004), 1119-1137. (IF: 1.327)
-Chen, Y., You, Z., and Tarnai, T.: Threefold-symmetric Bricard linkages for deployable –structures. International Journal of Solids and Structures 42 (2005), 2287-2301. (IF: 1.327)

Könyvek:

-Post-Buckling of Elastic Structures (Ed.: J. Szabó, Zs. Gáspár, T. Tarnai). Akadémiai Kiadó, Budapest / Elsevier Appl. Sci. Pub., Amsterdam, 1986.
-Spherical Grid Structures. Geometric Essays on Geodesic Domes (Ed.: T. Tarnai). Hungarian Institute for Building Science, Budapest, 1987.
-Summation Theorems in Structural Stability (Ed.: T. Tarnai). CISM Courses and Lectures No. 354. Springer-Verlag, Wien, New York, 1995

Kitüntetések, díjak:

Kiváló Munkáért (1986), Akadémiai Díj, Magyar Tudományos Akadémia (1988), TDK Munkáért Emlékplakett, Budapesti Műszaki Egyetem (1996), School of Architecture Kyoto University Emlékérme (1997), Tsuboi Award of the International Association for Shells and Spatial Structures (2002), Pioneers Award of University of Surrey, UK (2002), Széchenyi-díj (2002)

Közéleti tevékenység:

Az Építőmérnöki Doktori Iskola vezetője (2001-), a GAMM tagja (1994-), a GAMM MNB titkára (1991-93), elnöke (1994-96), tagja (1997-), az MTA Elméleti és Alkalmazott Mechanikai Bizottsága tagja (1991-), az IUTAM MNB tagja (1991-), a TMB, majd MTA Doktori Tanács Építés- Építészeti és Közleked.tud. Szakbiz. tagja (1992-2000), a CISM Scientific Council tagja (1993-2000), a CISM MNB tagja (1992-), az IASS WG No. 5 elnökhelyettese (1992-), az IASS Végrehajtó Tanács tagja (2004-), EUROMECH tagja (1995-), FKFP zsűrielnöke (1997-2001). Szerkesztőbizottsági tag: International Journal of Space Structures (1984-), Journal of Theoretical Graphics and Computing (1988-90), HyperSpace (1993-), International Journal of Solids and Structures (1996-2005), International Journal of Structural Stability and Dynamics (2000-), FORMA (2004-)

TARNAI TIBOR

Tarnai Tibor építőmérnök, alkalmazott matematikus, egyetemi tanár, a Magyar Tudományos Akadémia rendes tagja. Nemcsak hazánkban, nemzetközileg is elismert szaktekintély. Életútja a Wikipédián (szabad enciklopédia) olvasható. Életéről, munkásságról beszélgettünk Tarnai Tanár Úrral:

Elért eredményei még nagyobb értékűvé válnak göröngyös életútjának fényében. A II. világháború után lezárták a határokat. Hatalmas, sokszor megoldhatatlan problémát jelentett egy-egy nemzetközi konferencián való részvétel. (Már egy nyugati ország nagykövetségére is csak munkahelyi engedéllyel lehetett bejutni, és utólagos jelentéstételre kötelezték a meghívottat. Előfordult, hogy Tarnai Tanár Úr, ha sikerült is kiutaznia a konferenciára, pénz nélkül érkezett, valutát szerezni lehetetlen volt. Megkérte, hogy küldjenek érte kocsit a repülőtérre, mert nem volt miből vonatjegyet vennie.) A külföldi publikálást is tiltotta az akkori kormányzat. Előzetes engedélyek sorát kellett beszerezni egy cikk leközléséhez. (Még a Magyar Nemzeti Bankhoz is kellett kérvényt benyújtani, annak ellenére, hogy már akkor sem kaptak a szerzők jogdíjat a folyóiratoktól.) A rendszerváltozás óta több a lehetőség, Tanár Úr is több külföldi egyetemen végezhetett kutatásokat (Cornell Egyetem, Stanford Egyetem, Cambridge, Exteri Egyetem, Tokió, Kiotó, Oxford, Zhejiang Egyetem).

Tarnai Tibor minden buktató ellenére örül, hogy legalább „időnként hagyták dolgozni”. Sokszor persze nem: hiába volt főállású kutató az Építéstudományi Intézetben, nem ő választhatta a kutatási témáját. A minisztérium utasítására intézete például az esztétikus dúcolások problémakörét vizsgálta. Az épületek károsodása miatt nagyon sok helyen volt (és van) szükség ideiglenes alátámasztásra. Előfordult, hogy embereknek a saját lakásukban dúcoszlopokat kellett kerülgetniük (esetenként rácsozással merevített dúcokat). Több megoldás is született (pl. teleszkóposan kihúzható rudakat feszítenek a födém alá), de egyik sem valósult meg soha. Az intézetben dolgozók sok ideje veszett kárba az ehhez hasonló felesleges feladatokkal.

Hatalmas lehetőség rejlett ezért az OTKA pályázatokban. Az alapítványt éppen azért hozták létre, hogy támogassák a kutatók saját kutatási témáit. (Azelőtt a kutatók csak olyan területen dolgozhattak, ami a beosztásuknak, munkahelyüknek megfelelt. Az OTKA pályázatok viszont finanszírozták akár egy élelmiszeripari kutató autókipuffogóval kapcsolatos kutatásait is, nem kellett, ezért a kutatónak munkahelyet változtatnia.) Lehetőség nyílt így interdiszciplináris kutatásokra is. Tarnai Tibor különböző tudományterületeket ötvözött kutatócsoportjában (mechanika, matematika, virulógia (orvostudomány)). Ekkor kezdhetett a szerkezeti topológiával foglalkozni. Ez a terület a mechanika és a matematika határárán ingadozik, azt vizsgálja, hogy hogyan változik a szerkezet viselkedése kicsiny geometriai megváltozás hatására. Esetenként apró változtatás is óriási hatással lehet a szerkezet állékonyságára. Ez a mechanikai módszer használható pl. a vírusok alaktani kutatásaihoz vagy segíthet megoldani matematikai problémákat is. (Ebben a témában írt első cikke is egy neves matematikai folyóiratban jelent meg.)

Sokak szemében absztraktnak tűnhetnek szerteágazó kutatási témái (több, mint 190 tudományos publikáció szerzője, ebből három könyv és három könyvfejezet), de még a legelvontabbakat is mind a valóság szülte. Dolgozott mérnökként, műszaki ellenőrként a Földalatti Vasút Vállalatnál, majd statikus irányító tervezőként a Buvátinál (Budapesti Várostervezési Iroda) és a Szegedi Tervező Vállalatnál. Gyakorló szerkezettervezőként, a munkái során felmerült problémákat választotta tudományos vizsgálódásának alapjául.

Egyik jelentős publikációjának témája (Rúdszerkezet lokális stabilitásának vizsgálata operátornyalábokkal. (1979)) a BUVÁTI-ból származik. Az Újpesti Tisztasági Fürdő fedett uszodájához 32 m hosszú acél rácsos főtartókat használtak. A tartókat helyszíni toldás nélkül, egyben gyártották és úsztatták le a Dunán, azonban a tervezőket aggasztotta a karcsú szerkezet helyére emelése. Pontos számítás nem létezett rácsos tartók stabilitásvizsgálatára, de valószínű volt, hogy beemeléskor a nyomott öv kifordul. Ennek elkerülésére Tarnai Tiborék feszítőműveket terveztek a nyomott övre. A kivitelezőt zavarták a feszítőművek az amúgy is problémás munkafolyamatnál, ezért megpróbálta a beemelést nélkülük. Elmondása alapján azonban már a megemeléskor annyira belengett a szerkezet, hogy mégis kénytelen volt a javasolt feszítőművekhez folyamodni. Tarnai Tibort ezúttal is, mint később annyi más alkalommal, a konkrét alkalmazás mellett a mögöttes probléma tovább foglalkoztatta. (A kérdés matematikailag is érdekes, mert olyan sajátértékfeladatra vezet, amely a ¸ paraméterben másodfokú.) Az elkészült publikációjának differenciálegyenletei és operátornyalábjai tehát a Síkbeli rácsos tartók stabilitását írják le.

Az origamihajtogatás is segíthet szerkezetek viselkedésének megértésében (Hajtogatott szerkezetek (2002)), gondoljunk csak a Műegyetem E épületének egyik „hajtogatott” födémére. Ez nemcsak Tarnai Tanár Úr véleménye, hanem a Tokiói Egyetem szerkezettervező tanszékének vezetője is ebben a témában folytat kutatásokat.

Japánhoz köthető másik érdeklődési területe is: Tarnai Tibor japán kosarakat gyűjt. Ez a „hobbi” sem magáért való, a kosarak fonatát geometriai illetve topológiai szempontból tanulmányozza. Közismert matematikai tény, hogy a teret nem lehet csupa hatszöggel lefedni. A focilabdában is 6 db ötszög található a hatszögek mellett. Egy híres japán építész tervezte bambusz csarnok mégis csupa hatszöggel készült (a valóságban csalni kellett, hogy összeálljon). Hogy lehet az, hogy egy magasan qualifikált építész nem tudja azt, amit minden egyszerű, tudatlan, utcasarki kosárfonó Japánban? Ugyanis a kosarak fonata (általában alul) mindig tartalmaz kellő számú ötszöget. Tarnai Tanár Úr vad gráfelméletet hívott segítségül a kosárfonatok titkának megfejtéséhez.

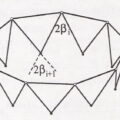
A térbeli rácsos tartók is hasonlíthatnak kosárhoz. Az IPARTERV a 70-es években Iránba tervezett acélszerkezetű hűtőtornyot. A csonakúp alapon álló henger acél rácsszerkezettel készült. Bár volt kezdetleges számítógépes programjuk térbeli rúdszerkezetek számítására, de ettől a toronytól a program „megbolondult”. A szakértőként felkért Kollár Lajos merevítőbordákat tetetett bele az állékonyság biztosítására, és megkérte Tarnai Tibort, hogy együtt keressék meg a szerkezet hibáját. Azért volt különös, hogy a szerkezet önmagában nem stabil, mert a felül szabad peremű henger elméletben képes membránállapotban viselni a terheket. Sőt Hegedűs Istvánnak ugyanebben az időben sikerült meghatároznia egy hasonló forgáshiperboloid rúderőit. Az ő szerkezete állékony volt (bár „beteg” szerkezetnek nyilvánította: a szomszédos rudak ellentétes előjelűek voltak, húzott-nyomott-húzott rudak váltogatták egymást). Miért nem tudott a hengeres hűtőtorony hasonlóan viselkedni? Tarnai Tibor fejtette meg. Egy aprócska eltérés miatt: alul páros számú rácspontot terveztek, míg az állékony forgáshiperboloidnak páratlan számú rácspontja volt. Kicsiny változás, ha megváltoztatja a statikai vagy kinematikai határozatlansági fokot alapjában befolyásolhatja a szerkezet viselkedését. Ilyen problémákat vizsgál a szerkezeti topológia. (Pl.: Kinematikailag határozatlan szerkezetek és szerkezeti topológia (1990) ).

Érdekesség, hogy ebben az időben a világon máshol is fel-felbukkant ez a probléma. Az űrhajók többlépcsőben leváló hordozó rakétáit is hasonló rácsszerkezet tartja. A rakéták leválásához szükséges, hogy a rácsos szerkezet mozogjon (ellentétben az épületszerkezetekkel, ahol a stabilitás a követelmény). Ezek a szerkezetek kivétel nélkül páros számú csomóponttal készülnek, bár a tervezőik nem tudják indokolni miért. Nem meglepő, hogy Tarnai Tanár Úr összes kutatási témája közül az ebben a témában írodott publikációi kaptak a legtöbb hivatkozást.

A szerkezeti topológia választ ad elhelyezési és fedési problémákra, biológiai és kémiai kérdésekre is. Segítségével lehetővé válik például optimális hálózat konstruálása geodetikus kupolák számára. Tarnai Tibor tehát képes matematikai eredményeket produkálni mechanikai megközelítéssel.

Elméleti munkássága mellett Tarnai Tibor az oktatásban is szerepet vállal. Gyakorlat vezetést pályája kezdetétől végez, ösztöndíjas aspiránsként, később félállasban tanított a Műszaki Egyetemen. Teljes munkaidőben a rendszerváltás után vállalt állást, először egy akadémiai kutatócsoport tagjaként, később egyetemi tanárként a Mechanika Tanszéken. Szeret tanítani. Bár néha vegyes érzések is ébrednek benne az oktatással kapcsolatban. Legjobban a PhD kurzus szabadon választható óráit kedveli. Itt érzi, hogy a hallgatók érdeklődése találkozik az általa felkínált lehetőségekkel. Tudományos iskolát teremtett, több oktatót és kutatót indított el és irányít ma is tudományos pályáján. Legnagyobb ellenérzései a vizsgáztatáshoz kötődnek: véleménye szerint itt „szembesül a kudarcaival”. Nyugtalanítják a felkészülés nélkül érkező hallgatók. Úgy érzi, hogy az új rendszer, hogy a hallgatók letölthetik az anyagokat az Internetről, elkényelmesít. A diákok kevesebbet járnak előadásra.

Szakmai közéleti tevékenysége is szerteágazó. Hat éven át volt tagja a CISM Scientific Council-nak, és jelenleg is társ elnöke az IASS Concrete Shells munkacsoportjának. Ezen túl több hazai és nemzetközi tudományos bizottság (Pl.: Műszaki Mechanikai Bizottság, majd Elméleti és Alkalmazott Mechanikai Bizottság, Tudományos Minősítő Bizottság, Doktori Tanács szakbizottsága …), konferencia szervező bizottság tagja, titkára, elnöke.

40 nemzetközi folyóiratnak dolgozott, ebből négynek – köztük a tekintélyes Journal of Solids and Stuctures – szerkesztő bizottsági tagja.

Tudományos, oktatási és tudományszervező tevékenységét külföldi és hazai kitüntetésekkel ismerték el. Ezek közül kiemelkedő az 1988. évi Akadémiai Díj és az 1997. évben odaítélt Kyoto Egyetem emlékérme.

1980-ban védte meg a műszaki tudományok kandidátusi, 1991-ben akadémiai doktori értekezését. Kiemelkedő tudományos tevékenységét elismerve a Magyar Tudományos Akadémia 2001- ben választotta rendes tagjai sorába.