Numerical analysis of the distance-controlled shape development of ellipsoids
The oldest known description of the shape development (wear) of naturally occurring inanimate objects (e.g. pebbles) comes from Aristotle. The mathematical model created on the basis of this description is called the radial distance-controlled model, which we know is rare in nature.
However, morphodynamics is still a well-researched field of science. A possible mathematical description of these processes is a parallel distance-controlled model related to the model of Aristotle, including perpendicular affinity.
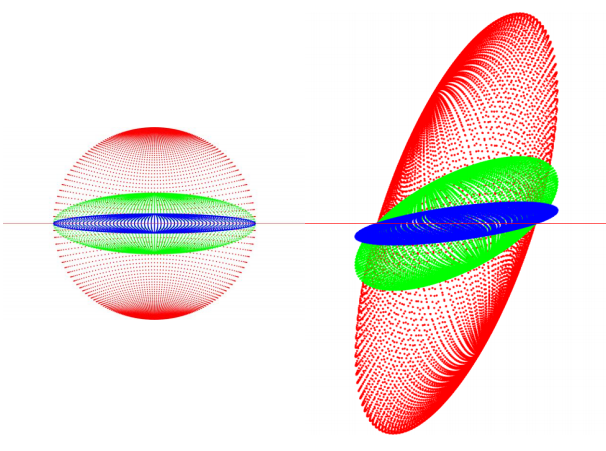
Visually, the wear of a pebble can be imagined so that the dots on the surface of the gravel, according to some rule, move in the direction of the inside of the gravel. Perpendicular affinity is such a model, because here the surface points of the body move towards the plane on lines that are unchanged in time, perpendicular to the plane intersecting the initial shape. The movement of the dots then depends only on the distance of the point from the plane.
The most common shape characteristics used in geology to describe shape development include the proportions of certain defined axes of the body and the isoperimetric ratio of the body, which shows a correlation between its volume and its surface area.
In the literature, changes in axis ratios have already been demonstrated in [1] the case of axial perpendicular affinity of a three-axis ellipsoid, but only conjectures have been formulated in case of general affinity. General case claims concerning the izoperimetric ratio have also been substantiated.
By preparing my thesis, my aim is to illustrate previously proven statements, on the other hand to examine conjectures by numerical methods, as well as to visually display the results.
For the preparation of my thesis, I used the optional subject “Mathematical modelling of mechanical tasks” and the material of my 2017 TDK thesis.
[1] Domokos, G. & Flame, Z., The Evolution of Geological Shape Descriptors Under Distance Driven Flows, Math Geosci (2018) 50: 337.