Falak stabilitásának vizsgálata az erők határozatlansága alapján
A falak a térelhatárolás alapvető szerkezetei. Stabilitásuk, tartósságuk elengedhetetlen jellemzőjük. Az emberiség az idők kezdete óta próbált minél ellenállóbb szerkezeteket létrehozni, így a falak geometriáját is úgy határozták meg, hogy minél szilárdabb struktúra jöjjön létre. Ennek legismertebb példája a téglafal: melynek esetében közel tízezer éve ismert, hogy a legerősebb falazat akkor készül, amikor a téglákat kötésben rakják.
„Falak geometriája” c. korábbi TDK dolgozatomban a konvex mozaikok átlagtér elméletének segítségével vizsgáltam a falazóelemek kontúrjából adódó fal-mozaikok geometriai tulajdonságait. A dolgozat legfontosabb eredménye, hogy a falazatokban lévő kötések geometriai megfontolások alapján a cellasűrűséggel (ρ) jellemezhetők, mely a stabilitás egy mérőszáma lehet.
Azonban a mozaik-elmélet nem tesz különbséget azonos cellasűrűségű ám eltérő geometriájú esetek között. Lehetséges ugyanis, hogy azonos cellafokszám és csomóponti fokszám mellett eltérő az elemek elrendezése. Például a fél téglával eltolt kötésben rakott fal cellasűrűsége ugyanúgy ρ=2,00, mint a negyed téglával eltolt fal esetében, ám a stabilitásukban mégis van különbség.
Célom, hogy egy általános, tetszőleges falra alkalmazható stabilitást jellemző mértéket definiáljak. Az alapvető ötlet, hogy azok stabil szerkezetek, ahol a téglák közti nyomóerők kis szórást mutatnak. Sem a túl kicsi, sem a túl nagy erő nem ideális a teherviseléshez, az előbbi nem képes oldalirányú terhelés elviselésére, az utóbbi az elemek túlterheléséhez vezethet.
Ehhez a kontakt dinamika algoritmus szimulációit alkalmaztam, ami a testre ható erőket úgy határozza meg, hogy azok az alapvető kényszerfeltételeknek (áthatolhatatlanság, súrlódás) eleget tegyenek. Mivel a rendszer határozatlan, ezért az algoritmus sztochasztikus volta miatt minden futtatás alkalmával egy másik véletlen, de stabil erőrendszert fog eredményezni, amiből a fent említett szórás számítható.
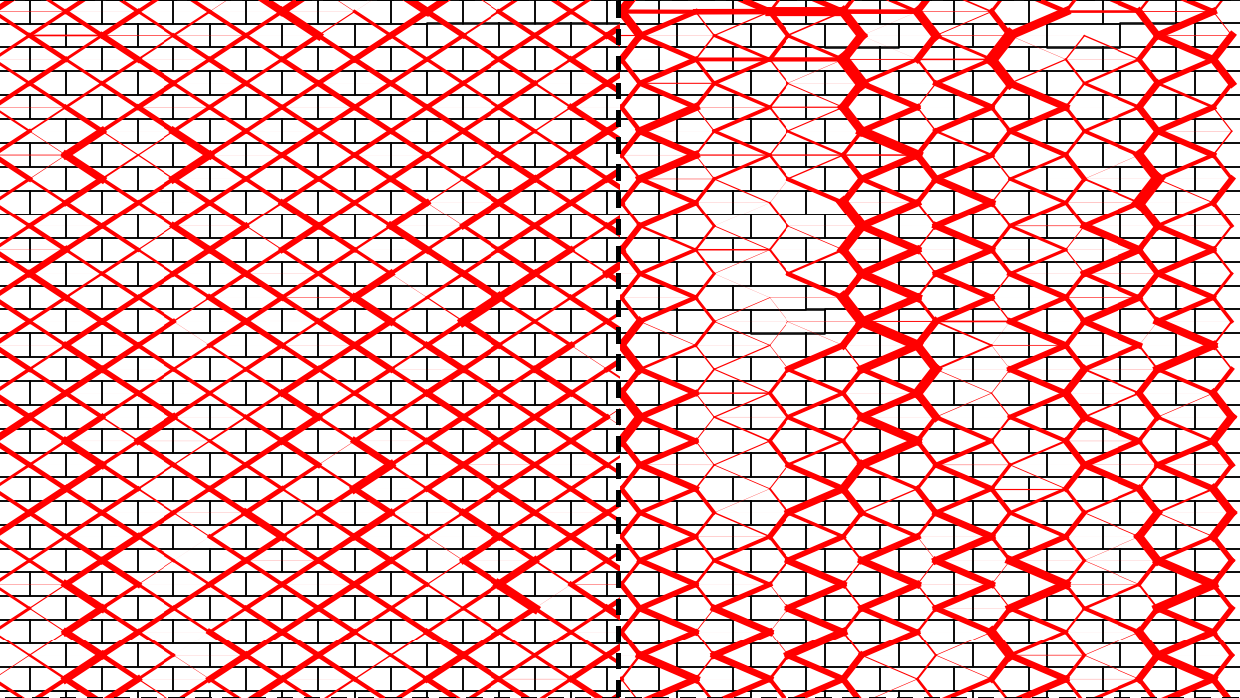
Az elgondolás demonstrálására a legismertebb példát – a téglafalat – vizsgáltam. Azt tapasztaltam, hogy a γ=1/2 esetén (bal oldali ábra) az erőhálózat szórása kicsi, az erők nagysága egyenletes, míg γ=1/4 esetében (kevésbé stabil kötésben, jobb oldali ábra) 57%-kal nagyobb szórás figyelhető meg.
Az általam bemutatott módszer kiterjeszthető tetszőleges geometriára, ezzel vizsgálható lesz a történeti falazatok stabilitása is.