Egy kétcsúcs tétel normális cella-felbontásokra
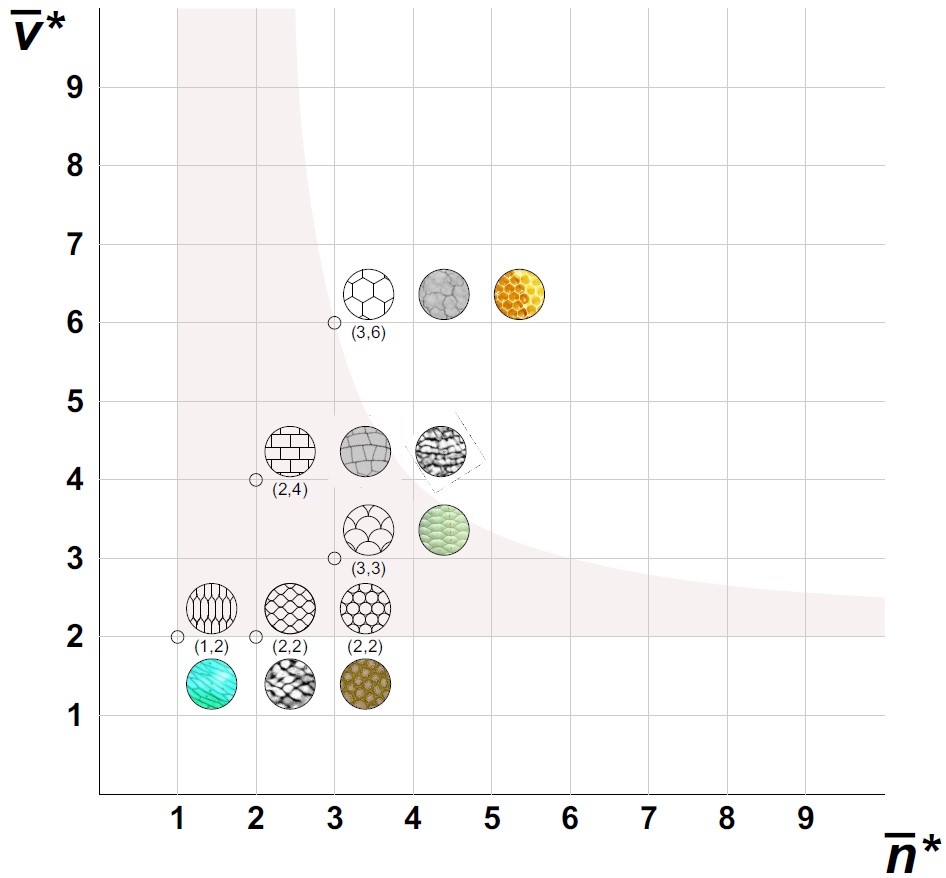
Nagyon sok természeti és mesterséges mintázat modelljeként használhatóak [1] a sima, beágyazott 2D sokaságok úgynevezett normális cella-felbontásai, ahol a cellák a körlappal homeomorfak, két cella metszete összefüggő halmaz (vagy az üres halmaz) és a cellák mérete egyenletesen korlátos alulról és felülről is. Megjelennek a biológiában, geológiában és kémiában. Az építészetben is gyakran találkozunk ilyen mintázatokkal: nem csak falazott szerkezetek vagy várostérképek modelljeiként szolgálhatnak, de a jól ismert mozaik képek matematikai leírására is alkalmasak. Ha egy ilyen mintázat celláit nem csak kombinatorikai, hanem metrikus tulajdonságaik alapján is vizsgáljuk, természetes, és az említett alkalmazások szempontjából különösen releváns módon vetődik fel a kérdés, hogy egy cellának átlagosan legalább hány „éles” csúcsa van, ahol az élek nem 180 fokban találkoznak. Megmutatjuk, hogy periodikus mintázatok esetén ez a minimális szám 2 és általános összefüggést adunk a minimális átlag, a hordozó sokaság Euler-karakterisztikája és a vizsgált cellafelbontás éleinek száma között.
[1] B. Grünbaum and G.C. Shepard, Tilings and Patterns, Freeman and Co., New York, 1987.