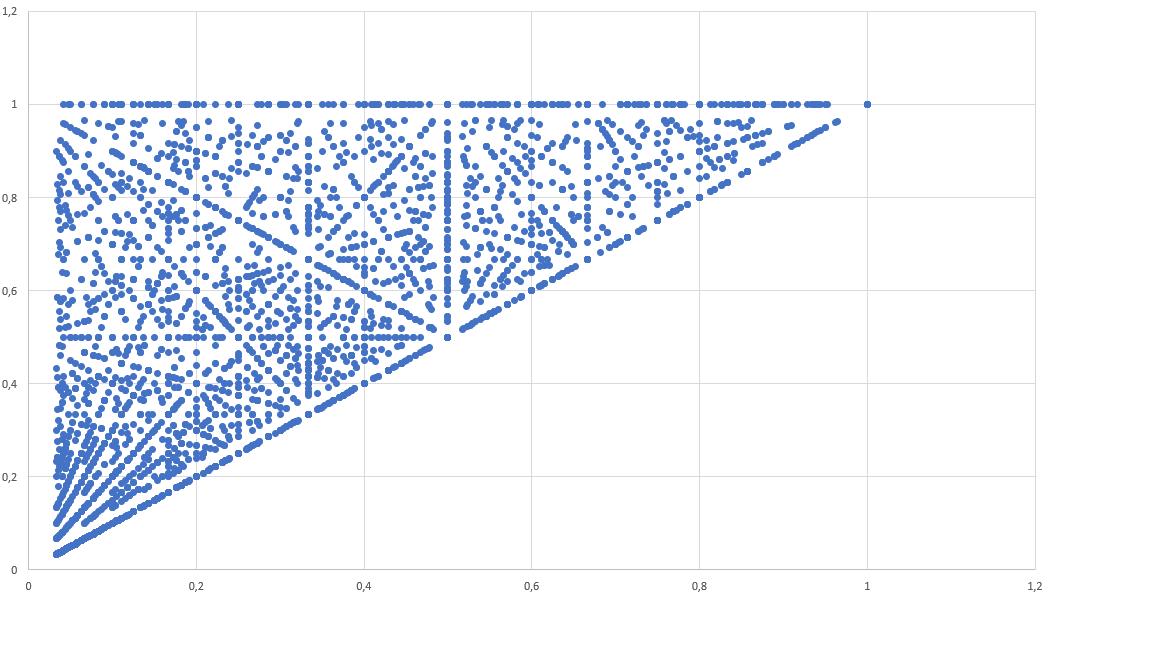
Geometriai mintázatok felbukkanása véletlen kavicspopuláció tengelyarányainak fázisterében
A kavicsok alakja sok információt hordoz a természetben lejátszódó eróziós folyamatokról, így például az üledékképződésről és a geofizikai transzport folyamatokról, emiatt a téma ma is a geomorfológiai kutatások homlokterében áll.
A geológiában számos osztályozási rendszer létezik a kavicsok morfológiájának leírására. Ezek közül a legrégebbi és legelterjedtebb a Zingg-féle osztályozás (1935) [1].
A Zingg-osztályozás a kavicsok alakját egy a≥b≥c tengelyhosszokkal rendelkező háromtengelyű ellipszoiddal közelíti, és ezt az (y1,y2)=(c/a, b/a) tengelyarányokra megadott intervallumok segítségével 4 osztályba sorolja. A Zingg-féle osztályozás alkalmazásakor a geológusok a terepen megmérik az a>b>c tengelyhosszakat és ezekből számítják a tengelyarányokat. Ilyen mérések akár több százezer kavics adatait is tartalmazhatják, például Carr 1969-ben az egyesült királyságbeli Chesil Beachen 100000 db kavics mérését végezte el.[2][3] Dolgozatomban a tengelyarányok terepen mért adatainak értelmezésével foglalkozom.
Mivel a mérés pontossága véges (a geológus a mért értékeket kerekíti), ezért feltesszük, hogy az a,b,c tengelyhosszok természetes számok. A terepi méréseket véletlen adathalmazzal közelítettem, vagyis feltettem, hogy a,b,c diszkrét, egyenletes eloszlású valószínűségi változók, rendre a [0,1…N], [0,1,…a],[0,1,…b] halmazokon. Egy így generált adathalmazhoz tartozó tengelyarányokat az [y1, y2] koordináta-rendszerben ábrázolva azt várnánk, hogy a pontok véletlenszerűen helyezkednek el. Ezzel szemben kirajzolódik egy mintázat, mintha a véletlen nem is lenne teljesen véletlen. Megfigyelhető, hogy az ábrázolt pontok egy része egyenesekre illeszthető. Dolgozatomban megmutatom, hogy ezen egyenesek természetes módon vannak jelen, ha ezek nincsenek ott, akkor lehet okunk gyanakodni arra, hogy a minta esetleg manipulált.
Dolgozatomban definiálom az [y1,y2] térben ábrázolt ponthalmaz egyeneseinek láthatóságát, továbbá ezen egyenesek meredekségét p/q relatív prím alakban veszem fel. Excel és a Matlab programok segítségével eltérő számosságú ponthalmazokat elemezve megállapítottam, hogy minél kisebb a (p,q) vektor normájának reciprokra, az egyenes annál inkább látható.
Irodalomjegyzék
[1] Zingg T.. 1935Beitrag zur Schotteranalyse. Mineral. Petrol. Mitte. 15, 39–140.
[2] Carr A. P.. 1969Size grading along a pebble beach: Chesil beach, England. J. Sedimentary Petrol. 39, 297–311.doi:10.1306/74D71C3A-2B21-11D7-8648000102C1865D (doi:10.1306/74D71C3A-2B21-11D7-8648000102C1865D).
[3] G. Domokos and G. W. Gibbons: 2012, The evolution of pebble size and shape in space and time, The Royal Society Publishing, https://doi.org/10.1098/rspa.2011.0562