Kölcsönhatás mentes kemény gömbök ütközési statisztikája
Manapság a fizika egyik legérdekesebb kihívása olyan komplex rendszerek viselkedésének előrejelzése, amik sok részecskéből állnak, és bár ezek között a kölcsönhatások egyszerűek, a kapott viselkedés igen szerteágazónak bizonyul (pl. esőfelhők, naprendszerek keletkezése, állatok csoportos mozgása, kavicsok kopása, stb.). A legtöbb ilyen tanulmány homogén, azonos tulajdonságú részecskékkel dolgozik, mert a probléma tovább bonyolódik, ha a rendszer részecskéinek tulajdonságai igen változatosak. Ilyen jellegű vizsgálat még a legegyszerűbb esetekben is kevés van.
A dolgozatban ezért egy olyan heterogén rendszer méretfüggő ütközési statisztikáját tanulmányozzuk, amelyben a részecskék között a tökéletesen rugalmas ütközésen kívül nincs kölcsönhatás. Elsőként a rendszert eseményvezérelt szimulációval vizsgáljuk, itt kiderül, hogy az ütközések száma a sugár függvényében nem monoton. A dolgozat hátralévő részében ezen görbe matetatikai leírásával foglalkozunk.
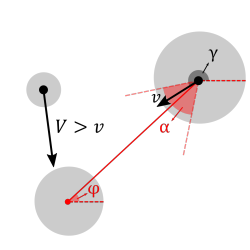
Modellünk lényege, hogy egy részecske ütközéseit a hozzá rögzített vonatkoztatási rendszerből vizsgáljuk, és föltesszük, hogy a többi (szabad) gömb bármely irányból, de csak az átlagos sűrűségből származtatott távolságból érkezhet. Ahhoz, hogy a tér egy adott irányából érkező szabad gömb ütközhessen a vizsgált gömbbel, sebességvektorának szöge csak egy bizonyos intervallumba eshet. A vizsgált gömb ütközési gyakoriságát az ütközési lehetőségek sebességgel súlyozott integráljaként kapjuk. Az integrál numerikus megoldásával kapott görbe közel tökéletesen megegyezik az eseményvezérelt szimuláció során látott görbével, több különböző sugáreloszlás esetén is.